handyfloss

La pregunta que da título a este post es bastante recurrente, o al menos me la he encontrado tanto que creo que merece la pena darle una respuesta lo suficientemente tajante y fundamentada como para despejar toda duda posible. A mí me parece bastante obvio que la respuesta correcta es que apagar la calefacción cuando no se necesita y encenderla luego para volver a calentar la casa es siempre más eficiente energéticamente que mantener la temperatura constante (y elevada) teniendo la calefacción constantemente encendida. Sin embargo existe gente que sigue defendiendo que el supuesto “gasto extra” de calentar la casa una vez enfriada de alguna manera hace que compense mantener siempre la temperatura. Demostraré matemáticamente en este post que dicho argumento es tan ridículo como el sentido común dicta.

Intentaré hacer este post lo más directo y resumido posible. Para un desarrollo algo más detallado, puedes bajarte las explicaciones en PDF.

Definición del problema

Vamos a proponer las siguientes convenciones:

• La temperatura en la casa es homogénea, T
• La temperatura caliente deseada es T_hot
• La temperatura exterior es T_cold (constante)
• El experimento comienza en un instante t₀, con el piso a T = T_hot
• En el Escenario 1, mantenemos la temperatura T constante
• En el Escenario 2 apagamos y luego encendemos la calefacción:
  • En t₀ apagamos la calefacción
  • Dejamos enfriar la casa hasta t₁, momento en que T habrá bajado hasta T₁
  • En t₁ encenderemos la calefacción, hasta alcanzar de nuevo T_hot en t = t₂

Nuestro objetivo será dilucidar en cuál de los 2 escenarios habrá tenido que aportar más calor al piso la calefacción. Para ello propondremos la Ecuación 1:

\(dQ = \alpha (T – T_{cold}) dt + q dT\)

En la Ecuación 1 hacemos un balance del calor, como la suma del calor perdido por el piso hacia el ambiente (primer término) y el empleado en elevar T (segundo término).

El calor perdido hacia el ambiente será proporcional a la diferencia de temperatura entre el piso y el ambiente, una constante de transferencia de calor (\(\alpha\)) y el intervalo de tiempo. El calor empleado en calentar el piso será proporcional a la capacidad calorífica del mismo (q) y el incremento de temperatura (dT).

Escenario 1: Temperatura constante

Usando la Ecuación 1, y manteniendo T en T_hot, obtendremos el valor de Q₁ (el calor total aportado en el Escenario 1) queda como se muestra en la Ecuación 2:

\(Q_1 = \alpha (T_{hot} – T_{cold}) (t_2 – t_1)\)

Escenario 2: Calefacción apagada y encendida

Mientras la calefacción está apagada, el aporte de calor será nulo, y la temperatura descenderá. Usando la Ecuación 1, obtendremos la evolución de la temperatura con la Ecuación 3:

\(T = T_{cold} + (T_{hot} – T_{cold}) e^{-\alpha t/q}\)

Cuando encendamos la calefacción la temperatura subirá de T₁ (valor hasta el que descienda T en el instante t₁) hasta T_hot entre t₁ y t₂. Para simplificar las ecuaciones supondremos que forzamos a la calefacción a producir tanto (o tan poco) calor como sea necesario para que la variación de la temperatura sea lineal con el tiempo.

La ecuación resultante para cuantificar el calor aportado durante esta fase (es decir el calor total para el Escenario 2, ya que en su primera fase la calefacción está apagada) es la Ecuación 4:

\(Q_2 = \alpha \frac{t_2 – t_1}{2}(T_{hot} + T_1 – 2 T_{cold}) +q (T_{hot} – T_1)\)

Recuerda que puedes seguir el desarrollo que conduce a esta ecuación en la versión en PDF.

Ejemplos

Comparararemos Q₁ y Q₂ en diferentes situaciones, ilustrando las comparaciones con 5 ejemplos. Las gráficas presentadas pueden reproducirse con el mismo script de Python que yo usé para generarlas, y que puedes bajarte pinchando aquí. Juega todo lo que quieras con los parámetros, y verás cómo es matemáticamente imposible que las líneas verdes superen a las rojas.

En el primer ejemplo variaremos el coeficiente de transmisión de calor (\(\alpha\)). Si lo hacemos, obtendremos la Figura 1:

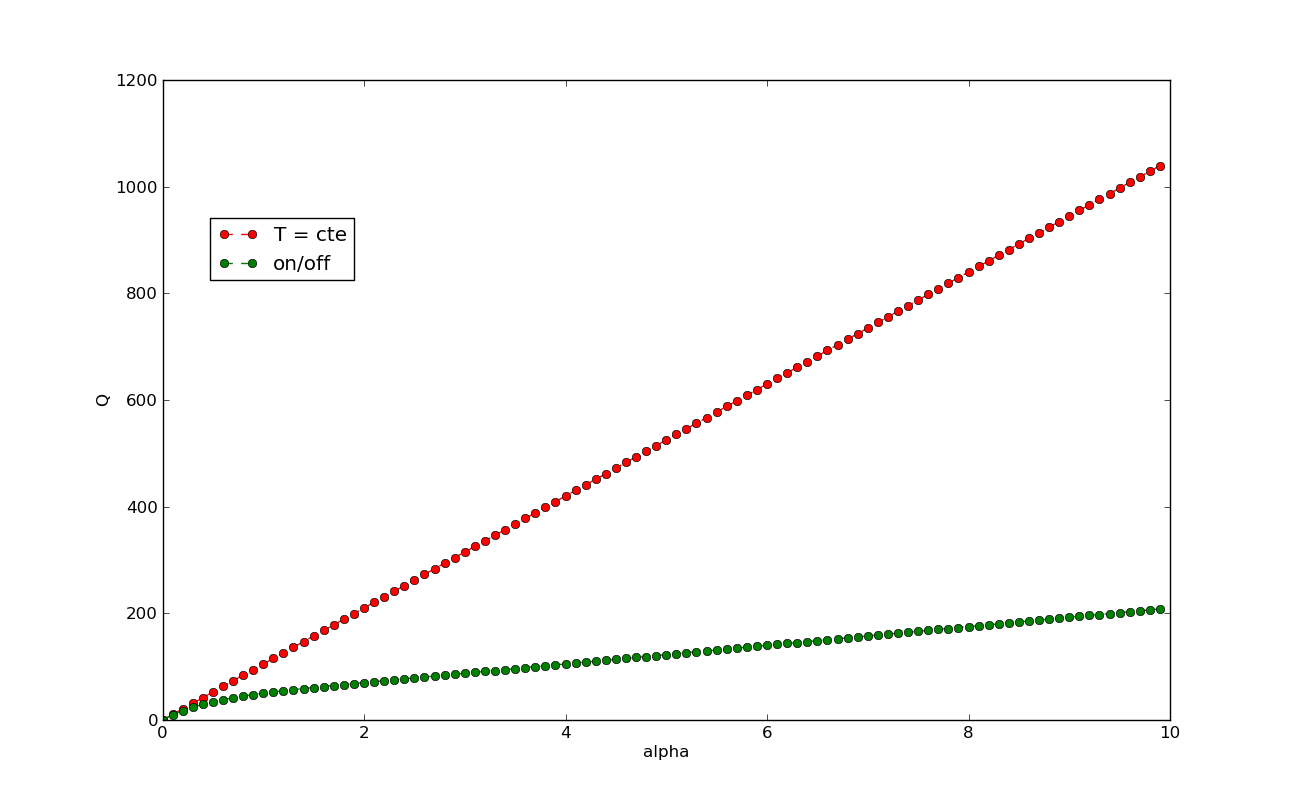
Como vemos en la Figura 1, a peor aislamiento (mayor \(\alpha\)), mayor aporte de calor en ambos casos, pero siempre más en el Escenario 1, y la diferencia crece con \(\alpha\). La única manera en que ambos escenarios necesiten el mismo aporte de calor es que el aislamiento sea perfecto (\(\alpha=0\)), pero en ese caso ambos escenarios darán un gasto de calor nulo (la temperatura se mantendrá sola).

En el segundo ejemplo variaremos la capacidad calorífica del piso (q). Este es el factor que hace a los ingenuos pensar que el Escenario 1 “podría” suponer un ahorro energético, porque en el Escenario 2 “cuesta más” subir la temperatura de nuevo hasta T_hot, que mantenerla en el Escenario 1.

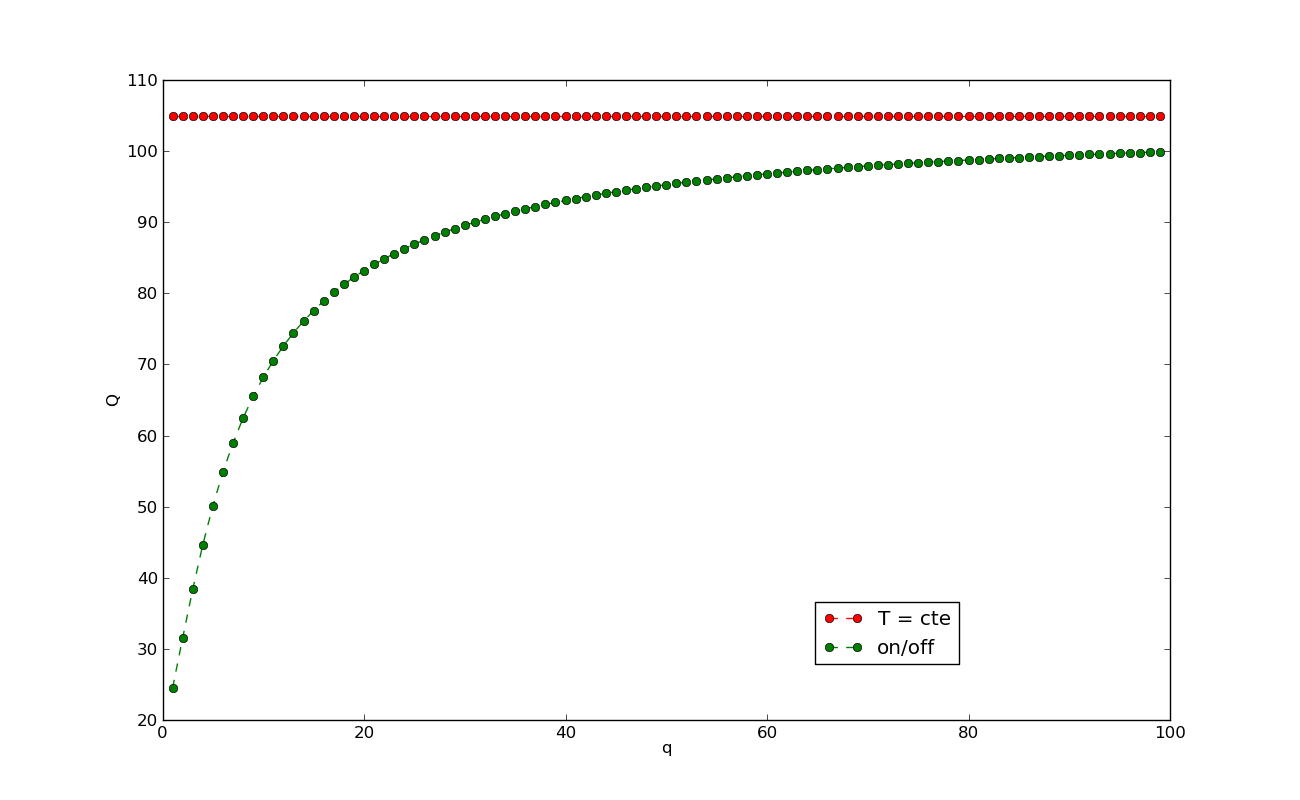
Como vemos en la Figura 2, es cierto que cuanto mayor sea q, menos ventajoso es el Escenario 2, pero siempre es ventajoso. Cuando aumentamos q, ciertamente aumentamos el calor requerido para recuperar T_hot, pero también reducimos la bajada de temperatura durante el tiempo que la calefacción está apagada.

En el tercer ejemplo variamos el tiempo que la calefacción está apagada en el Escenario 2. El tiempo que estará la calefacción encendida luego se mantiene constante.

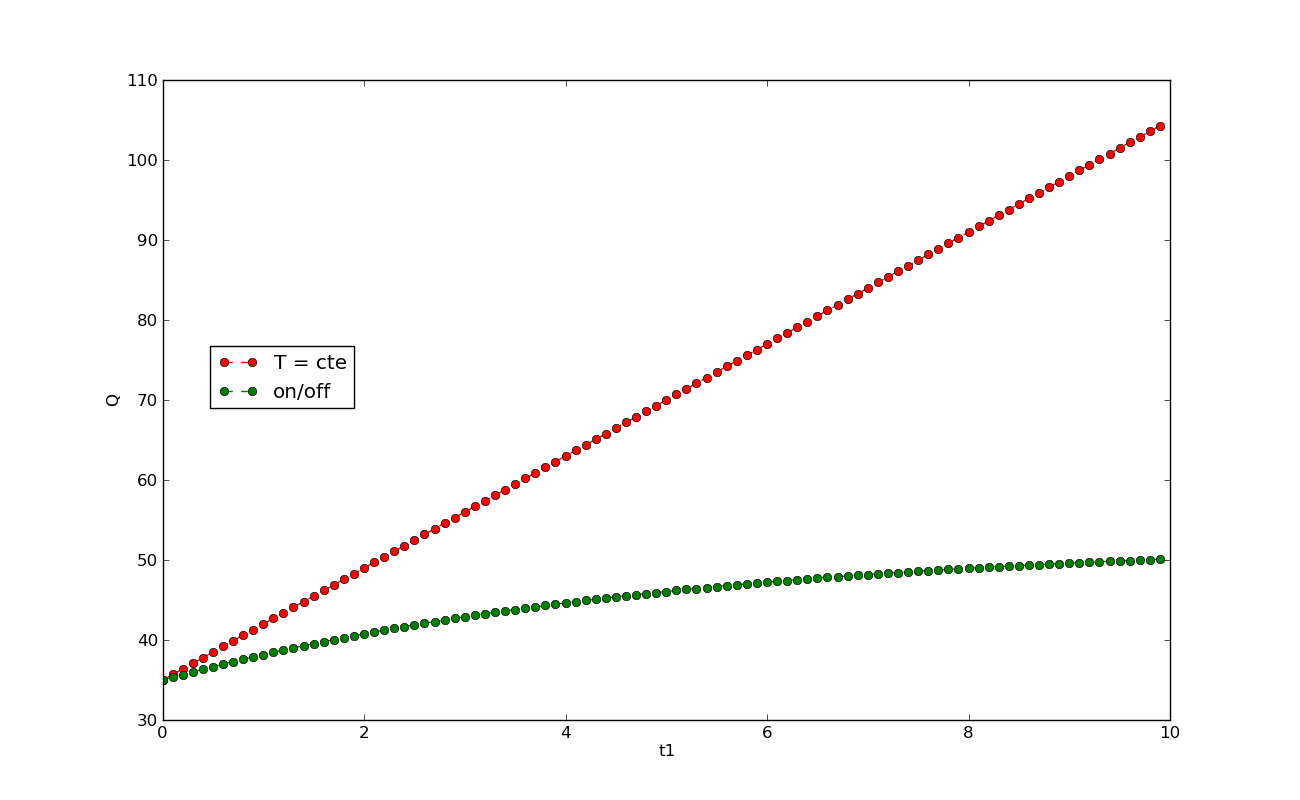
Al aumentar t₁ el calor del Escenario 1 aumenta (ya que aumenta el tiempo total). En el Escenario 2 también aumenta, pero de manera mucho menor. De hecho en función de q puede incluso disminuir (si q es pequeño).

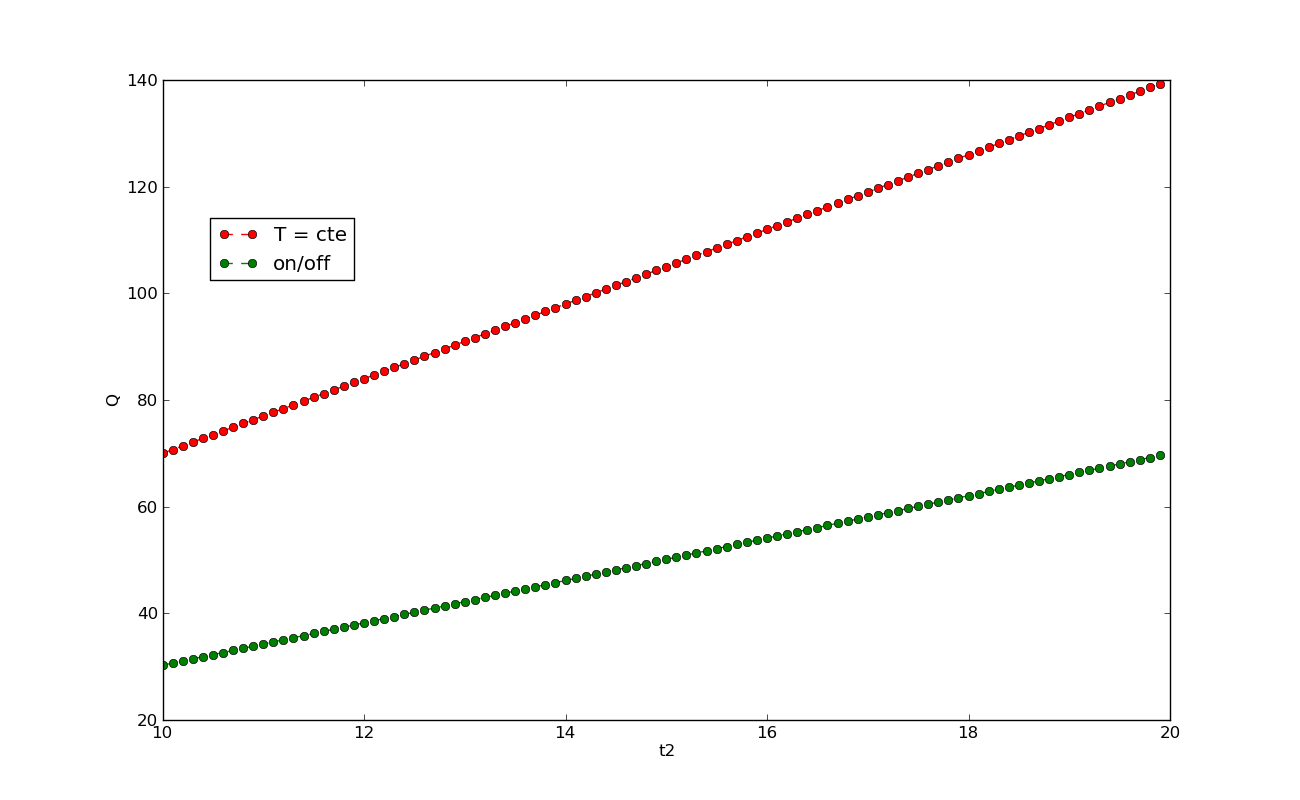
En el cuarto ejemplo variaremos el tiempo que tenemos la calefacción encendida en el Escenario 2 (manteniendo t₁ constante). Aquí también aumenta el consumo para ambos Escenarios, pero el incremento es mayor siempre para el Escenario 1.

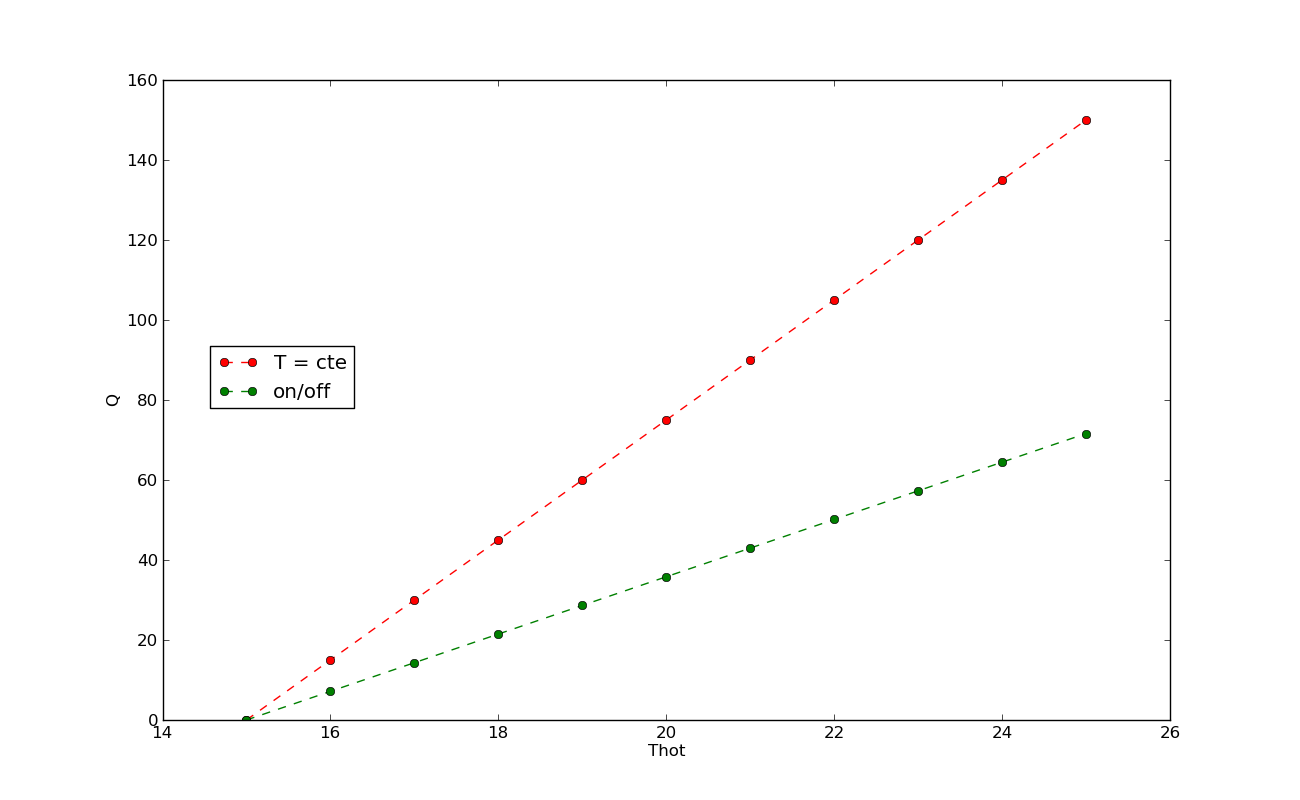
En el quinto y último ejemplo variaremos la temperatura cálida deseada (T_hot). En el Escenario 1 el gasto de calor es directamente proporcional a esta temperatura (en realidad, a la diferencia de esta con T_cold). Como podemos ver en la Figura 5, en el Escenario 2 también se da esta relación lineal, pero como vemos la constante de proporción es menor. La única manera de que el gasto del Escenario 2 sea igual al del 1 es que la temperatura T_hot sea igual a T_cold, en cuyo caso el gasto en ambos escenarios es cero (no hace falta encender la calefacción para mantener el piso a la temperatura de la calle).

Conclusiones

Como no podía ser de otra manera, hemos visto que el gasto de calor es siempre superior si mantenemos la temperatura del piso constante y elevada mediante calefacción continua.

La lógica de este resultado es sencilla y deja poco lugar a duda. El calor perdido por el piso aumenta al aumentar la temperatura, con lo cual el gasto máximo ocurrirá cuando se mantenga todo el rato la temperatura elevada. Si el piso pasa mucho tiempo frío (cuando no estamos en casa), y sólo un poco de tiempo caliente (cuando lo necesitamos), las pérdidas totales (y por tanto el consumo de calefacción) serán mucho menores, y cuando más tiempo pase frío, más ahorro. Cierto es que cuando encendamos la calefacción habrá que recuperar la temperatura perdida mientras estaba apagada, pero reflexionemos lo siguiente: el aporte de calor que tendremos que dar para ello será igual al calor perdido mientras estaba apagada, ¡nunca superior! El único añadido a ese calor que damos es el necesario para compensar en cada momento el calor que se pierde por transferencia al ambiente, que siempre será mayor en el Escenario 1, puesto que en él la temperatura en cada instante es igual o superior a la del Escenario 2.